Get to know about the rules and strategies to solve Sudoku from easy to very hard. Every strategy has an explanation and an example showing how to use it. Here is our full strategy list: Naked Singles, Hidden Singles, Naked Pairs, Hidden Pairs, Pointing Pair, Crossing Pairs, X-Wings and XY-Wings. This guide was written by the former Italian Sudoku Grandmaster Gabriele Simionato.
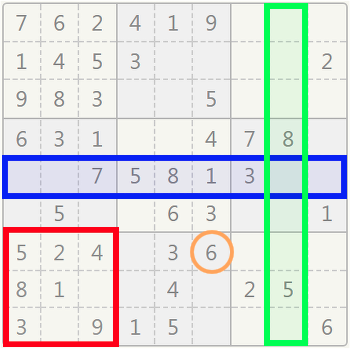
Here you can see a typical sudoku grid. It consists of 9 rows, 9 columns and 9 sectors. You can see a row (in blue), a column (in green) and a sector (in red) highlighted here on the right. Sectors, rows and columns overlap each other.
There are 81 cells. Some of them already have numbers ("given digits") and they cannot be changed. In the orange circle you can see a "given digit". Every cell is part of a row, a column AND a sector.
Your goal is to fill the blank cells so that each row, column, and sector contains numbers 1-9 without repetitions.
The digits you added are marked in red. You can always delete a red number if you spot a mistake.
If this is the first time you see a completed sudoku, check for its validity:
If all the conditions are met, the grid is solved correctly.

This brings us to the idea of a CANDIDATE DIGIT.
While given digits are fixed, you can choose in the blank cells among their candidates.
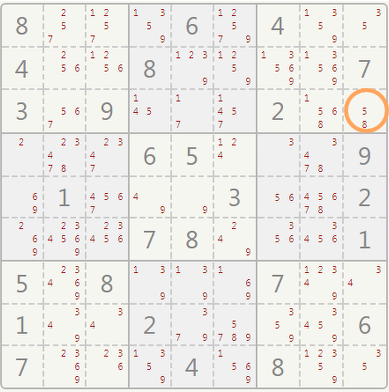
A number is NOT a candidate in a cell if it appears again in the same row, column, or sector that contains that cell. Check the cell in the orange circle: digits 2, 4, 7 are NOT candidates because they appear in the same sector. Digits 2, 3, 9 are NOT candidates because they appear in the same row. Digits 1, 2, 6, 7, 9 are NOT candidates because they appear in the same column.
The leftovers, 5 and 8 are the candidates for this cell.
The following strategies will help you to solve Sudoku puzzles from very easy to very hard. It will probably take some time to learn them but they will make you a great Sudoku player.
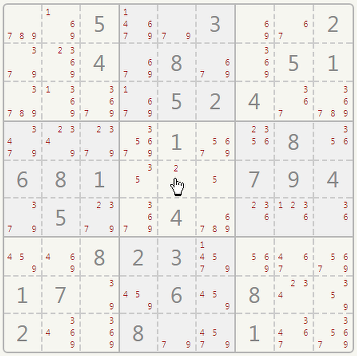
A NAKED SINGLE is spotted when a cell, anywhere in grid, contains a single candidate. Look at the cell where the mouse pointer is: the only candidate is number "2".
So, this is the only possibility left for this cell: click on it and select number "2" from the keypad.
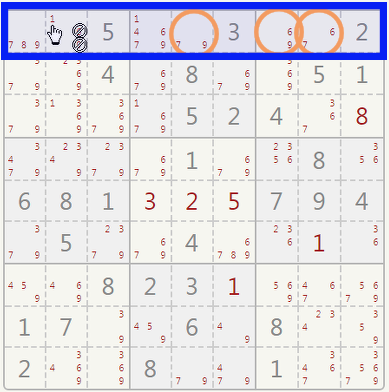
A HIDDEN SINGLE is spotted if:
Example:
Check the upper right sector (in red). Where can you write the number 8 within this sector? Since it appears already in the two columns marked in green, there's only one cell left for the 8.

A NAKED PAIR is spotted if:
Example:
Check the upper row (in blue). The first and last cell both have the same pair of candidates: 1 and 2. This means that if there's a 1 in the leftmost cell, there is a 2 in the rightmost one, and vice versa. In both cases, since you cannot have twice the same number in a row, you can cross off all the other 1s and 2s that appear in that row.
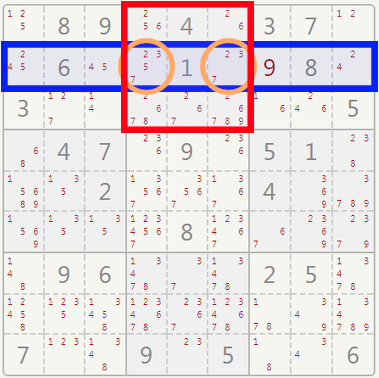
A HIDDEN PAIR is spotted if:
Example:
Check the row in blue. There are five blank cells but where could you put numbers 3 and 7 in this row? Only the cells marked in orange show 3 and 7 among their candidates. This means that no other numbers can be written in these cells: they are reserved to 3 and 7. Mentally cross off the other candidates in the cells marked in orange.
Look for three cells in the same row, which contain the same three candidates, or a subset of the same three candidates.
In our example, three cells can contain only digits 6, 7, 9. Although there are many combinations in which this could be done, such digits cannot appear again in other cells of the same row/column/sector. Look at the examples below:
You can mentally cross off the 6 and the 9 from the cell where the pointer is, leaving it with a single candidate.
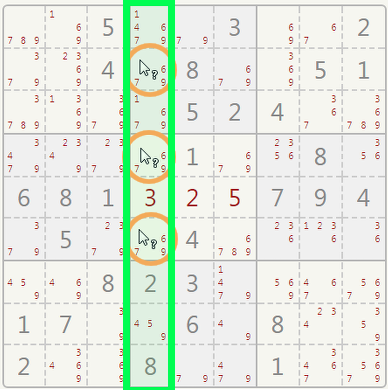
You can mentally cross off the 6, 7, and 9 from the other cells in this column. They can't be candidates in cells other than the orange ones.
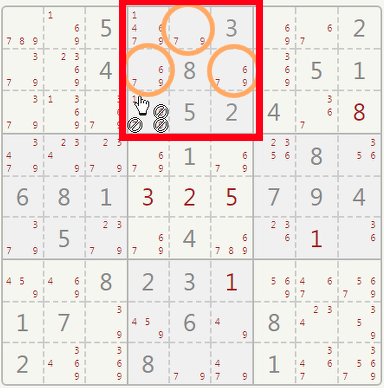
You can mentally cross off the 6, 7, and 9 from the other cells in this sector. They can't be candidates in cells other than the orange ones.
Because of this reduction, you can certainly put a "1" in the cell where the pointer is.
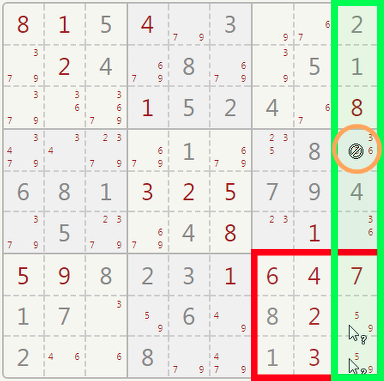
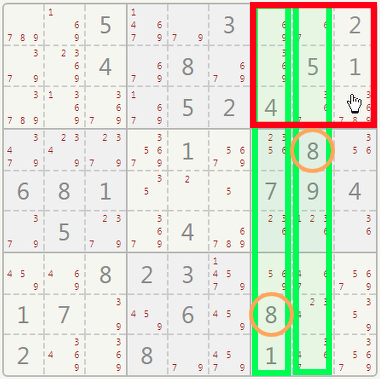
A POINTING PAIR is usually spotted in a sector.
Example:
Two cells in the same sector (in red) can have digits 5 and 9. Although you cannot immediately decide which number goes where, you can see that 5 and 9 cannot appear again in the same column.
Cross off the 5 in the orange cell. Doing so will, in turn, create another POINTING PAIR which will reduct further candidates in the same sector.
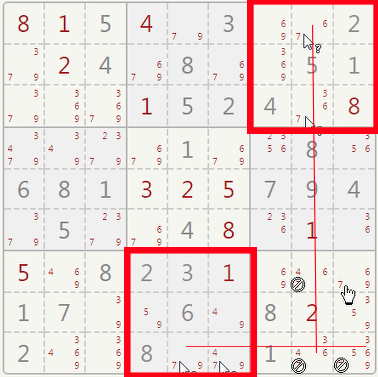
You can use the knowledge gained with the previous strategies to apply advanced techniques to your sudoku grid. Checking the two red sectors will show you that the possible positions for number 7 are on a line.
This allows you to mentally cross off all the 7s which appear again on the same line outside the sectors. In the bottom right sector only one spot remains for number 7.
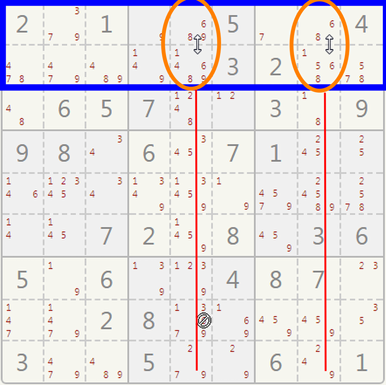
X-WINGS are very hard to spot, but they help you in the final stages of a harder sudoku. You have to look for two rows in which a candidate appears twice in the same columns.
Example:
Check for number 6 in the blue area. It can appear only in the orange circles.
Since the 6 appears there, it cannot appear again along the same two columns, so you can cross the 6s off the red lines.
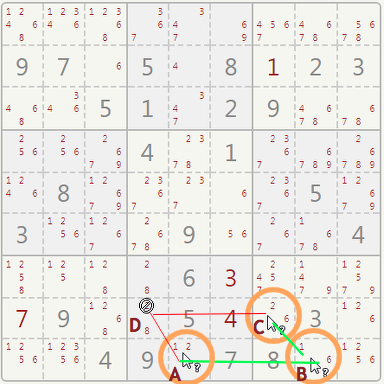
XY-WINGS are placed in three connected cells which share pairs of candidates in the form of: XY-XZ-YZ, hence the name.
Example:
In our example, the three cells ABC have a pair of candidates: (1, 2), (1, 6) and (2, 6).
If A has a 2, then the 2 must be crossed off from D. If A has a 1, then B has a 6, C has a 2 and again D can't have a 2. No matter what goes into A, you can definitely cross off the 2 from D.